PRÁCTICA 2: SERIES DE FOURIER y TRANSFORMADA DE FOURIER
1 Series de Fourier.
1.1 Funciones periódicas.
Maxima tiene varias sentencias para calcular las series de Fourier de funciones
periódicas que están disponibles en el paquete "fourie".
Para usarlas, previamente hemos de cargar dicho paquete tecleando la siguiente
instrucción:
| --> | load("fourie"); |
MAXIMA nos dará un mensaje indicándonos que el paquete ha sido cargado.
Una vez cargado, si queremos calcular la serie de Fourier de una función
periódica f(t) de periodo T, entonces si tomamos L = T/2, entonces la sentencia
fourier(f(t),t,L)
nos devuelve una lista con los coeficientes de Fourier de dicha función.
NOTA: No se da la serie completa, sino los coeficientes
a_0, a_n, b_n,
por ejemplo, si tenemos la siguiente función:
f1(t)= t+t^2 con -2≤ t ≤2
| --> | f1(t) := t+t^2; |
cuya representación es:
| --> | wxplot2d(t+t^2,[t,-2,2]); |
Si la repetimos periódicamente con periodo T=4 y por tanto L = T/2 = 2. es decir
f1(t) = f1(t+4) para todo t
Gráficamente:
| --> | g1(t) := f1(t+4)*(unit_step(t+6)-unit_step(t+2))+f1(t)*(unit_step(t+2)-unit_step(t-2))+f1(t-4)*(unit_step(t-2)-unit_step(t-6)); |
| --> | wxplot2d(g1(t),[t,-6,6]); |
Nota: Sólo se definen 3 periodos completos.
Calculamos los coeficientes de su serie de Fourier mediante el siguiente comando:
| --> | fourier(f1(t),t,2); |
Observamos que la respuesta de la función es ligeramente distinta a las respuestas
usuales de MAXIMA, los coeficientes son devueltos en variables que comienzan
con "%t" y finalmente la respuesta del sistema en las variables usuales "%o", que es una
lista que contiene los coeficientes de las variables %t anteriores.
%t hace referencia a una variable temporal.
Nota: Podemos comprobar que el programa no utiliza las propiedades trigonométricas
del seno y coseno para ángulos que son múltiplos de pi.
Sabemos que la función seno toma valores 0 en los argumentos múltiplos de pi, es decir, sabemos que
sin(nπ) = 0
sin embargo:
| --> | sin(n*%pi); |
Mientras que para la función coseno, estos valores serían (-1)^n, sin embargo:
| --> | cos(n*%pi); |
Para hacer uso de estas propiedades trigonométricas se utiliza la función
foursimp(expresion)
que está relacionada con dos variables del sistema:
sinnpiflag
cosnpiflag
Por defecto, los valores de estas variables son "true", como podemos comprobar
si usamos dichas variables
| --> |
sinnpiflag; cosnpiflag; |
De esta forma si utilizamos la instrucción foursimp junto con fourier tendremos:
| --> | foursimp(fourier(f1(t),t,2)); |
1.2 FUNCIONES PARES E IMPARES
| --> |
kill(all)$ load(fourie)$ |
Como sabemos, las series de Fourier tienen una forma especial para el caso de funciones pares e impares,
ya que en estos casos los coeficientes del seno o coseno se hacen nulos, respectivamente.
FUNCIONES PARES: Si f(t) es periódica de periodo T y es una función par, es decir
f(-t) = f(t),
entonces dicha función solo tendrá coeficientes coseno no nulos y su serie la podemos obtener como
fourcos(f(t),t,T)
EJEMPLO:
| --> |
f2(t):=t^2; wxplot2d(f2(t),[t,-2,2]); |
Si repetimos periódicamente con T=4 y L=2
| --> |
g2(t) := f2(t+4)*(unit_step(t+6)-unit_step(t+2))+f2(t)*(unit_step(t+2)-unit_step(t-2))+f2(t-4)*(unit_step(t-2)-unit_step(t-6)); wxplot2d(g2(t),[t,-6,6]); |
Y su serie de Fourier se obtiene como:
| --> | fourcos(f2(t),t,2); |
O simplificando
| --> | foursimp(fourcos(f2(t),t,2)); |
Vemos que no se incluyen los coeficientes b_n.
También podemos utilizar la función fourier:
| --> | fourier(f2(t),t,2); |
donde podemos comprobar que los coeficiente b_n son nulos.
FUNCIONES IMPARES: Si f(t) es periódica de periodo T y es una función impar, es decir
f(-t) = -f(t),
entonces dicha función solo tendrá coeficientes seno no nulos y su serie la podemos obtener como
foursin(f(t),t,T)
EJEMPLO:
| --> |
f3(t):=t^3; wxplot2d(f3(t),[t,-2,2]); |
Si repetimos periódicamente con T=4 y L=2
| --> |
g3(t) := f3(t+4)*(unit_step(t+6)-unit_step(t+2))+f3(t)*(unit_step(t+2)-unit_step(t-2))+f3(t-4)*(unit_step(t-2)-unit_step(t-6)); wxplot2d(g3(t),[t,-6,6]); |
Y su serie de Fourier se obtiene como:
| --> | foursin(f3(t),t,2); |
O simplificando
| --> | foursimp(foursin(f3(t),t,2)); |
Vemos que no se incluyen los coeficientes a_n.
También podemos utilizar la función fourier:
| --> | fourier(f3(t),t,2); |
donde podemos comprobar que los coeficiente a_n son nulos.
1.3 EXTENSIONES PARES E IMPARES
| --> |
kill(all)$ load(fourie)$ |
Recordemos que una función f(t) definida en un intervalo [0,L] la podemos extender periódicamente de forma PAR e IMPAR
EXTENSIÓN PAR:
Si la extendemos de forma par en [-L,L] y la hacemos 2L-periódica a toda la recta real.
Dicha función solo tendrá coeficientes coseno no nulos y su serie la obtendremos como
fourcos(f(t),t,T),
EXTENSIÓN IMPAR:
Si la extensión de f(t) a [-L,L] se hace de forma impar y la hacemos 2L-periódica a toda la recta real,
la serie sólo tendrá coeficientes seno que se calculan con la sentencia:
foursin(f(t),t,T)
C:\Silvestre\public_html\am_ti\practicas\Extension.jpg
Figura 1:

EJEMPLO: Calcula la serie de Fourier de la función
f(t) = exp(-t)*sin(2*t) en [0,%pi],
cuando se extiende de forma periódica par e impar.
Definimos y representamos la función en el intervalo [0,%pi]:
| --> |
f(t) := exp(-t)*sin(2*t); f_plot(t) := f(t)*(unit_step(t)-unit_step(t-%pi)); wxplot2d(f_plot(t),[t,0,%pi]); |
Su extensión par se define como:
| --> |
f_par(t) := f(-t)*(unit_step(t+%pi)-unit_step(t))+f(t)*(unit_step(t)-unit_step(t-%pi)); wxplot2d(f_par(t),[t,-%pi,%pi]); |
Aquí representamos 3 periodos consecutivos:
| --> |
f_parext(t) := f_par(t+2*%pi)*(unit_step(t+3*%pi)-unit_step(t+%pi))+f_par(t)*(unit_step(t+%pi)-unit_step(t-%pi))+f_par(t-2*%pi)*(unit_step(t-%pi)-unit_step(t-3*%pi)); wxplot2d([f_parext(t),f_par(t)],[t,-3*%pi,3*%pi]); |
y su extensión impar será:
| --> |
f_impar(t) := -f(-t)*(unit_step(t+%pi)-unit_step(t))+f(t)*(unit_step(t)-unit_step(t-%pi)); wxplot2d(f_impar(t),[t,-%pi,%pi]); |
donde hemos representado también 3 periodos consecutivos:
| --> |
f_imparext(t) := f_impar(t+2*%pi)*(unit_step(t+3*%pi)-unit_step(t+%pi))+f_impar(t)*(unit_step(t+%pi)-unit_step(t-%pi))+f_impar(t-2*%pi)*(unit_step(t-%pi)-unit_step(t-3*%pi)); wxplot2d([f_imparext(t),f_impar(t)],[t,-3*%pi,3*%pi]); |
A continuación calculamos sus respectivas series de Fourier:
EXTENSIÓN PAR:
| --> | foursimp(fourcos(f(t),t,%pi)); |
EXTENSIÓN IMPAR:
| --> | foursimp(foursin(f(t),t,%pi)); |
NOTA: Si utilizáramos la función fourier directamente sobre f(t):
| --> | foursimp(fourier(f(t),t,%pi)); |
Estaríamos calculando la serie de Fourier de la función
| --> |
f_ext(t) := f(t+2*%pi)*(unit_step(t+3*%pi)-unit_step(t+%pi))+f(t)*(unit_step(t+%pi)-unit_step(t-%pi))+f(t-2*%pi)*(unit_step(t-%pi)-unit_step(t-3*%pi)); f_interv(t) := f(t)*(unit_step(t+%pi)-unit_step(t-%pi)); wxplot2d([f_ext(t),f_intrev(t)],[t,-3*%pi,3*%pi]); |
Notar que se repite de forma periódica los valores de f(t) en el intervalo [-pi, pi].
Si sólo queremos repetir periódicamente el intervalo [0,%pi]
| --> | wxplot2d(f(t),[t,0,%pi]); |
Entonces en ese caso la función debe definirse utilizando la función de Heaviside como:
| --> |
fc(t) := f(t)*(unit_step(t)-unit_step(t-%pi))$ fc_ext(t) := fc(t+%pi)*(unit_step(t+%pi)-unit_step(t))+fc(t)*(unit_step(t)-unit_step(t-%pi))+fc(t-%pi)*(unit_step(t-%pi)-unit_step(t-2*%pi)); wxplot2d(fc_ext(t),[t,-%pi,2*%pi]); |
Pero como veremos más adelante, para calcular su serie de Fourier no es posible utilizar la función fourier, por la presencia de la función unit_step.
1.4 CONSTRUCCIÓN DE LA SERIE DE FOURIER
| --> |
kill(all)$ load(fourie)$ |
Si tenemos los coeficientes de Fourier de una cierta función T-periódica hasta un cierto
valor n (pudiendo éste ser ∞, esto es inf), podemos construir su serie de Fourier, o mejor dicho,
una aproximación de esta con la sentencia fourexpand que tiene la sintaxis
fourexpand(lista,t,L,n)
donde lista es el conjunto de los coeficientes de Fourier, calculados previamente,
t es la variable independiente, L es la mitad del periodo y n es el número de términos
que queremos en el desarrollo. Realmente n indica el número de pares (coseno/seno)
de la serie de Fourier.
EJEMPLO: Vamos a constuir los desarrollos en series de Fourier de la función
f(t) = t + t^2
con n=2.
Calculamos en primer lugar los coeficientes de la serie y asignamos dichos valores a una variable
que utilizaremos después.
| --> |
f(t):= t+t^2; coeficientes:foursimp(fourier(f(t),t,2)); |
A continuación realizamos la reconstrucción para n=2
| --> | fourexpand(coeficientes,t,2,2); |
Notar que para este valor de n=2, se obtienen 5 valores que corresponden a los términos
a_0, (a_1, b_1) y (a_2, b_2).
Podemos ver qué ocurre cuando se incrementa el número de términos. Para ello
vamos a definir las funciones que se obtienen cuando en el desarrollo usamos
la serie con n=5, n=10 y n=50 coeficientes.
Para n=5:
| --> |
sf1(t):=fourexpand(coeficientes,t,2,5); sf1(t); |
Obtenemos 11 términos (término independiente, 5 términos coseno y 5 términos seno).
Para n=10:
| --> |
sf2(t):=fourexpand(coeficientes,t,2,10); sf2(t); |
Obtenemos 21 términos (término independiente, 10 términos coseno y 10 términos seno.
Para n=50:
| --> |
sf3(t):=fourexpand(coeficientes,t,2,50); sf3(t); |
Obteniéndose en este caso 101 términos.
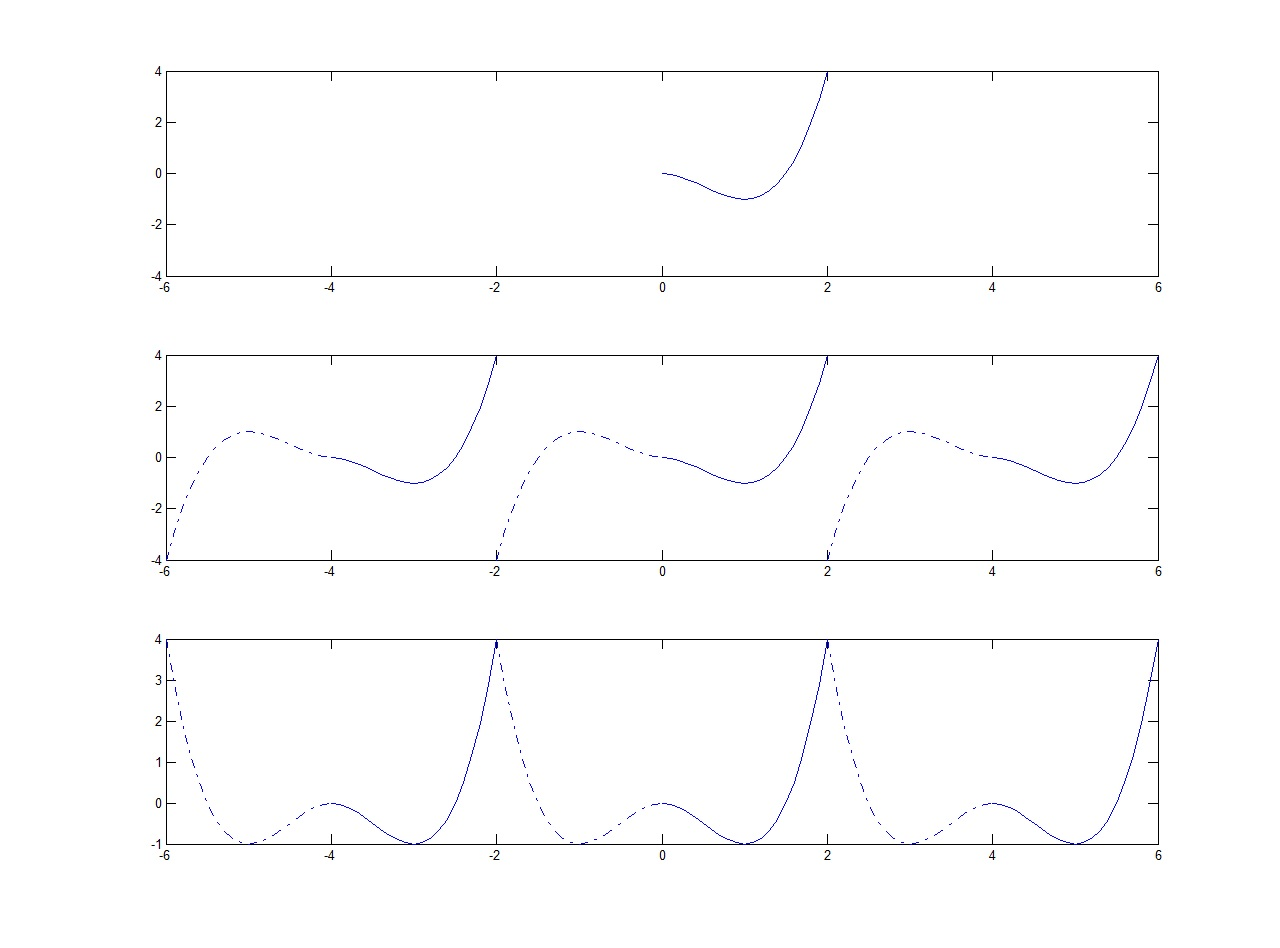
Veamos sus representaciones gráficas comparadas con la de f(t):
| --> | wxplot2d([f(t),sf1(t)],[t,-2,2]); |
| --> | wxplot2d([f(t),sf2(t)],[t,-2,2]); |
| --> | % |
| --> | wxplot2d([f(t),sf3(t)],[t,-2,2]); |
Notar lo que ocurre en los extremos de la función. Aunque aumente el número de términos
en el sumatorio, en los puntos de discontinuidad la diferencia se acentúa (fenómeno Gibbs).
| --> | wxplot2d([f(t),sf1(t),sf2(t),sf3(t)],[t,-2,2]); |
APROXIMACIONES DE LAS EXTENSIONES PAR E IMPAR
Vemos lo que ocurre con las extensiones PAR e IMPAR al aumentar el número de términos en la reconstrucción.
Definimos y representamos la función en el intervalo determinado:
| --> |
f(t) := exp(-t)*sin(2*t); f_plot(t) := f(t)*(unit_step(t)-unit_step(t-%pi)); wxplot2d(f_plot(t),[t,0,%pi]); |
y construímos sus extensiones par e impar:
| --> |
f_par(t) := f(-t)*(unit_step(t+%pi)-unit_step(t))+f(t)*(unit_step(t)-unit_step(t-%pi)); f_impar(t) := -f(-t)*(unit_step(t+%pi)-unit_step(t))+f(t)*(unit_step(t)-unit_step(t-%pi)); wxplot2d([f_plot(t),f_par(t),f_impar(t)],[t,-%pi,%pi]); |
EXTENSIÓN PAR:
Calculamos los coeficientes de la extensión par:
| --> | coef_par : fourcos(f(t),t,%pi); |
Definimos las aproximaciones correspondientes para diferentes valores de n:
Para n=5 (6 términos, desde a_0 hasta a_5):
| --> |
sf1p(t):=fourexpand(coef_par,t,%pi,5)$ sf1p(t); |
Para n=10 (11 términos, desde a_0 hasta a_10):
| --> |
sf2p(t):=fourexpand(coef_par,t,%pi,10)$ sf2p(t); |
Para n=50 (51 términos, desde a_0 hasta a_50):
| --> |
sf3p(t):=fourexpand(coef_par,t,%pi,50)$ sf3p(t); |
Y representamos gráficamente comparando con f(t):
| --> |
wxplot2d([f_plot(t),sf1p(t)],[t,-%pi,%pi]); wxplot2d([f_plot(t),sf2p(t)],[t,-%pi,%pi]); wxplot2d([f_plot(t),sf3p(t)],[t,-%pi,%pi]); |
O si comparamos todas las gráficas en el intervalo donde deben coincidir con f(t):
| --> | wxplot2d([f_plot(t),sf1p(t),sf2p(t),sf3p(t)],[t,0,%pi]); |
Notar que las distintas aproximaciones se acercan a la gráfica de la extensión par:
| --> |
f_parext(t) := f_par(t+2*%pi)*(unit_step(t+3*%pi)-unit_step(t+%pi))+f_par(t)*(unit_step(t+%pi)-unit_step(t-%pi))+f_par(t-2*%pi)*(unit_step(t-%pi)-unit_step(t-3*%pi)); wxplot2d([f_parext(t),sf1p(t),sf2p(t),sf3p(t)],[t,-3*%pi,3*%pi]); |
EXTENSIÓN IMPAR:
Calculamos los coeficientes de la extensión impar:
| --> | coef_impar: foursin(f(t),t,%pi); |
Definimos las aproximaciones correspondientes para diferentes valores de n:
Para n=5 (5 términos, desde b_1 hasta b_5):
| --> |
sf1i(t):=fourexpand(coef_impar,t,%pi,5);$ sf1i(t); |
Para n=10 (10 términos, desde b_1 hasta b_10):
| --> |
sf2i(t):=fourexpand(coef_impar,t,%pi,10)$ sf2i(t); |
Para n=50 (50 términos, desde b_1 hasta b_50):
| --> |
sf3i(t):=fourexpand(coef_impar,t,%pi,50)$ sf3i(t); |
Y representamos gráficamente comparando con f(t)
| --> |
wxplot2d([f(t),sf1i(t)],[t,-%pi,%pi]); wxplot2d([f(t),sf2i(t)],[t,-%pi,%pi]); wxplot2d([f(t),sf3i(t)],[t,-%pi,%pi]); |
Como antes, en los tres casos, la función y las extensiones se aproximan a f(t) en el intervalo [0,L]=[0,%pi]
| --> | wxplot2d([f(t),sf1i(t),sf2i(t),sf3i(t)],[t,0,%pi]); |
Las diferentes aproximaciones se acercan a la extensión impar de la función f(t)
| --> |
f_imparext(t) := f_impar(t+2*%pi)*(unit_step(t+3*%pi)-unit_step(t+%pi))+f_impar(t)*(unit_step(t+%pi)-unit_step(t-%pi))+f_impar(t-2*%pi)*(unit_step(t-%pi)-unit_step(t-3*%pi)); wxplot2d([f_imparext(t),sf1i(t),sf2i(t),sf3i(t)],[t,-3*%pi,3*%pi]); |
SERIE FOURIER COMPLETA
Es posible utilizar el infinito para obtener la serie de Fourier completa.
Por ejemplo para la función
f(t) = t + t^2; con t en [-2,2]
| --> |
kill(all)$ load(fourie)$ f(t):=t+t^2$ coeficientes:foursimp(fourier(f(t),t,2))$ fourexpand(coeficientes,t,%pi,inf); |
Esta operación puede hacerse automáticamente con la sentencia totalfourier cuya sintaxis es:
totalfourier(f(t),t,L)
y que devuelve la serie de Fourier completa.
La sentencia:
| --> | totalfourier(f(t),t,2); |
es equivalente a:
| --> | fourexpand(foursimp(fourier(f(t),t,2)),t,2,'inf); |
1.5 FUNCIONES CONTINUAS A TROZOS
| --> |
kill(all)$ load(fourie)$ |
Todo lo que se ha visto anteriormente, no funciona si queremos calcular la serie de Fourier de
una función continua a trozos. Si por ejemplo, consideramos la la siguiente función
definida en el intervalo [-2,2]
f(t) = 2+t para -2≤ t < 0
f(t) = 2-t para 0≤ t < 2
| --> |
sierra(t):= (2+t)*(unit_step(t+2)-unit_step(t))+(2-t)*(unit_step(t)-unit_step(t-2))$; wxplot2d(sierra(t),[t,-3,3]); |
Y supongamos que la repetimos periódicamente, con periodo T=4 y semiperiodo L=2.
La representación gráfica para 3 periodos sería:
| --> |
sierrap(t) := sierra(t+4)*(unit_step(t+6)-unit_step(t+2))+sierra(t)*(unit_step(t+2)-unit_step(t-2))+sierra(t-4)*(unit_step(t-2)-unit_step(t-6)); wxplot2d(sierrap(t),[t,-6,6]); |
Si ahora tratamos de calcular sus coeficientes de Fourier con las funciones correspondientes:
| --> | fourier(sierra(t),t,2); |
Vemos que la respuesta de MAXIMA no es nada satisfactoria. El problema surge por la presencia de la función
unit_step(t).
Para calcular los coeficientes debemos utilizar la definición de los mismos mediante integrales:
Así el coeficiente a_0 sería (tomando L=2)
L
a_0 = 1/L ∫ f(t) dt
-L
que para este caso sería:
2
a_0 = 1/2 ∫ sierra(t) dt
-2
que al ser a trozos, debe calcularse como:
| --> | a0: a[0] = ((integrate(2+t,t,-2,0)+integrate(2-t,t,0,2))/2)/2; |
Hemos definido una variable a0 que contiene el elemento 0 del vector a, además hemos incluido el
factor 1/2 que lleva la fórmula de Fouier.
Los coeficientes a_n serían (para L=2)
L
a_n = 1/L ∫ f(t)cos(nπt / L) dt
-L
que para este caso sería:
2
a_n = 1/2 ∫ sierra(t) cos( nπt / 2) dt
-2
y que al ser a trozos, debe calcularse como:
| --> | an: a[n] = (integrate((2+t)*cos(n*%pi*t/2),t,-2,0)+integrate((2-t)*cos(n*%pi*t/2),t,0,2))/2; |
Los coeficientes a_n serían (para L=2)
L
b_n = 1/L ∫ f(t)sin(nπt / L) dt
-L
que para este caso sería:
2
b_n = 1/2 ∫ sierra(t) sin(nπt / 2) dt
-2
y que al ser a trozos, debe calcularse como:
| --> | bn: b[n] = (integrate((2+t)*sin(n*%pi*t/2),t,-2,0)+integrate((2-t)*sin(n*%pi*t/2),t,0,2))/2; |
Notar que la función es par y por eso los b_n son ceros.
Construimos la lista de coeficientes utilizando las variables creadas en el proceso anterior:
| --> | lista : [a0,an,bn]; |
Podemos aproximar la serie por el número de términos que queramos usando fourexpand:
| --> |
sierra_aprox(t):= fourexpand(lista,t,2,5); sierra_aprox(t); |
Y ya podemos comparar con la función original
| --> | wxplot2d([sierra(t),sierra_aprox(t)],[t,-2,2]); |
Por ejemplo si n=50
| --> |
sierra_aprox2(t):= fourexpand(lista,t,2,5); wxplot2d([sierra(t),sierra_aprox2(t)],[t,-2,2]); |
Podemos ver lo que ocurre para 3 periodos:
| --> |
sierrap(t) := sierra(t+4)*(unit_step(t+6)-unit_step(t+2))+sierra(t)*(unit_step(t+2)-unit_step(t-2))+sierra(t-4)*(unit_step(t-2)-unit_step(t-6)); wxplot2d([sierrap(t),sierra_aprox2(t)],[t,-6,6]); |
La "culpa" de que no se puedan utilizar las funciones fourier, fourcos o foursin es de la función unit_step(t) cuya primitiva no está definida
en MAXIMA:
| --> | integrate(unit_step(t),t); |
2 Transformada de Fourier
| --> |
kill(all)$ load(fourie)$ |
No hay ninguna función especial para el cálculo de la transformada de Fourier de una función; es necesario usar la integración directa.
Por ejemplo para la función
-|t|
f(t) = e
| --> | f(t):=exp(-abs(t)); |
| --> | F:integrate(exp(t)*exp(-%i*w*t),t,-inf,0)+integrate(exp(-t)*exp(-%i*w*t),t,0,inf); |
| --> | ratsimp(gfactor(F)); |
Calcularemos la transformada de Fourier de las siguientes funciones:
a) g(t) = exp(-at)*h0(t) con a>0
b) h(t) = A si -T≤ t ≤ T, f(t)=0 resto
c) k(t) = exp(-a t*t) con a>0
a)
| --> |
assume(a>0); g(t) := exp(-a*t)*unit_step(t); G(w) := integrate(0*exp(-%i*w*t),t,-inf,0)+ integrate(exp(-a*t)*exp(-%i*w*t),t,0,inf); G(w); |
Borramos la asunción hecha sobre a.
| --> | forget(a>0); |
b)
| --> |
assume(T>0); h(t) := A*(unit_step(t+T)-unit_step(t-T)); H(w) := integrate(A*exp(-%i*w*t),t,-T,T); H(w); |
| --> | trigreduce(rectform(H(w))); |
| --> | forget(T>0); |
c)
| --> |
assume(a>0); k(t) := exp(-a*t*t); K(w) := integrate(k(t)*exp(-%i*w*t),t,-inf,inf); K(w); |
| --> | forget(a>0); |
| --> | fourint(k(t),t); |
3 Ejercicios para practicar.
PROBLEMA 1. Obtener los desarrollos de Fourier y de seno y coseno de orden 10 e infinito de las funciones siguientes:
1. cos(t) definida en [0,π].
2.sin(2t) definida en [0,π].
3.t³ definida en [0,1].
4. t*e^{t} definida en [0,6].
5 .cos t definida en [0,2π].
PROBLEMA 2. Encuentre los desarrollos en serie de Fourier de orden 10 de las siguientes funciones periódicas (se da su valor en el intervalo [-L,L] con 2L el periodo).
1. f(t) = {
-1 si t ∈[-1,0),
1 si t ∈[0,1]
2. f(t) = {
t si t ∈[-2,0),
0 si t ∈[0,2]
3. f(t) = t si t ∈[-1,1]
4. f(t) = {
-t si t ∈[-1,0),
t si t ∈[0,1]
5. f(t) = {
1 si t ∈[-2,0),
0 si t ∈[0,1),
1 si t ∈[1,2]
PROBLEMA 3. Calcula la transformada de Fourier de las siguientes funciones:
1. f(t) = {
cos(t) si t ∈[-pi/2, pi/2],
0 resto
2. f(t) = {
t si t ∈[-a,a],
0 resto
3. f(t) = {
a-t si t ∈[-a,a],
0 resto
4. f(t) = {
0 si t ≤ -2,
-1 si t ∈(-2,-1),
1 si t ∈(-1, 1),
-1 si t ∈(1,2),
0 si t≥2
5. f(t) = {
sen(a*t) si t ∈[-pi/a,pi/a),
0 resto